yolov5+csl旋转目标检测代码解析2

本篇主要记录学习yolov5+csl旋转目标检测的原理，主要是探究代码中如何得到theta/gauss_theta的target。参考知乎略略略 https://zhuanlan.zhihu.com/p/358441134； yangxue https://zhuanlan.zhihu.com/p/111493759

一、debug记录

经过dataloader之后的数据格式如图，cls已经转化为id。此时仍是原本的表示方法。
图片描述
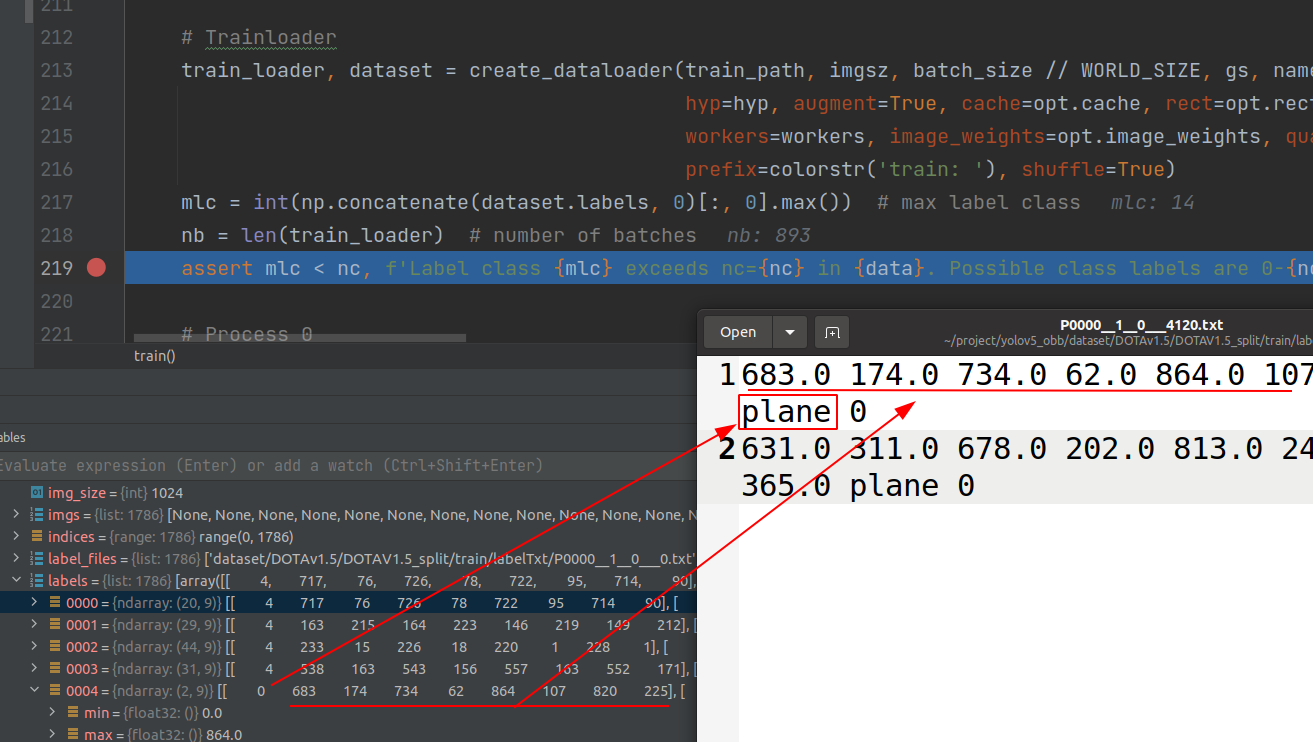
在plot_labels里面会有完整的标签格式转换以及高斯窗的csl方法，但是这个函数并没有返回

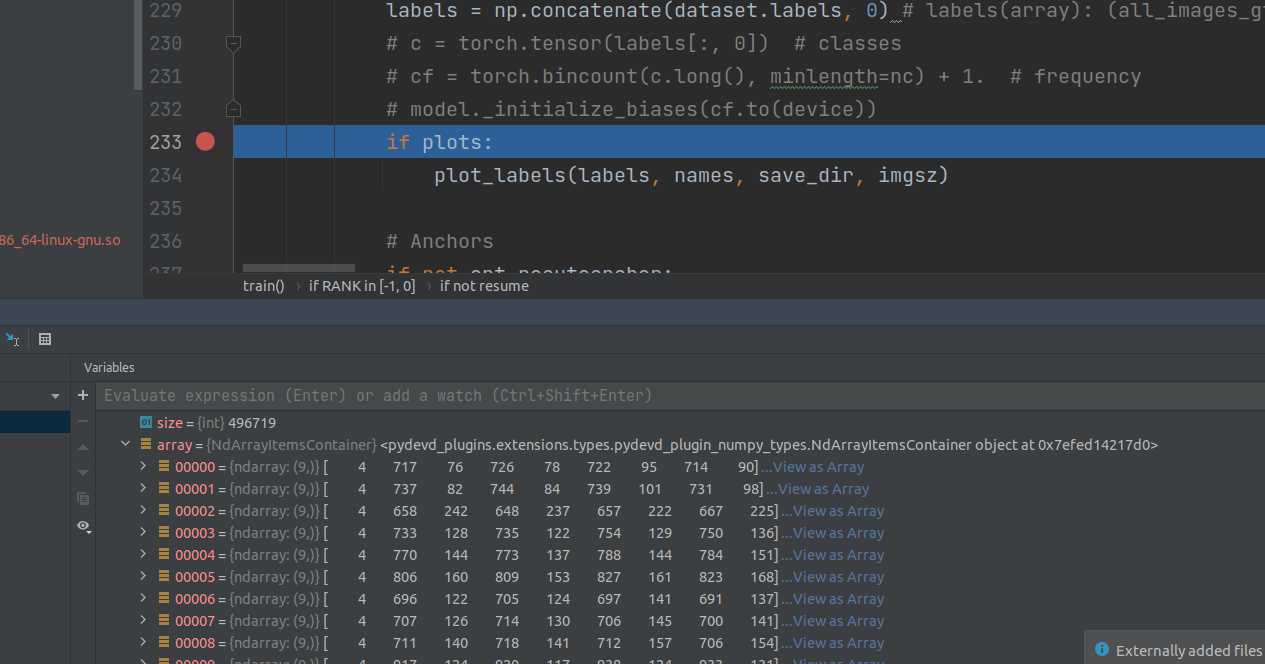
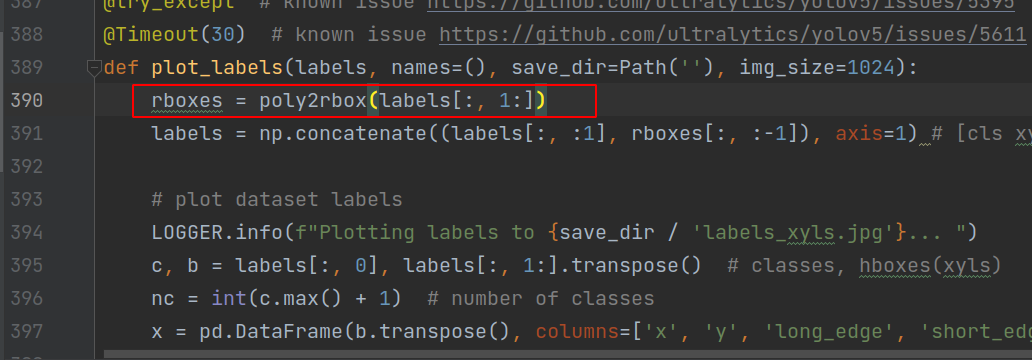
即最后一个参数为True时，使用csl，并且采用高斯窗函数，csl部分代码是直接从yangxue大佬那里拿来用的。

def poly2rbox(polys, num_cls_thata=180, radius=6.0, use_pi=False, use_gaussian=False):
    """
    Trans poly format to rbox format.
    Args:
        polys (array): (num_gts, [x1 y1 x2 y2 x3 y3 x4 y4]) 
        num_cls_thata (int): [1], theta class num
        radius (float32): [1], window radius for Circular Smooth Label
        use_pi (bool): True θ∈[-pi/2, pi/2) ， False θ∈[0, 180)

    Returns:
        use_gaussian True:
            rboxes (array): 
            csl_labels (array): (num_gts, num_cls_thata)
        elif 
            rboxes (array): (num_gts, [cx cy l s θ]) 
    """

数据处理（转换标签格式，生成theta参数等操作），在LoadImagesAndLabels类中重写了getitem方法。
图片描述
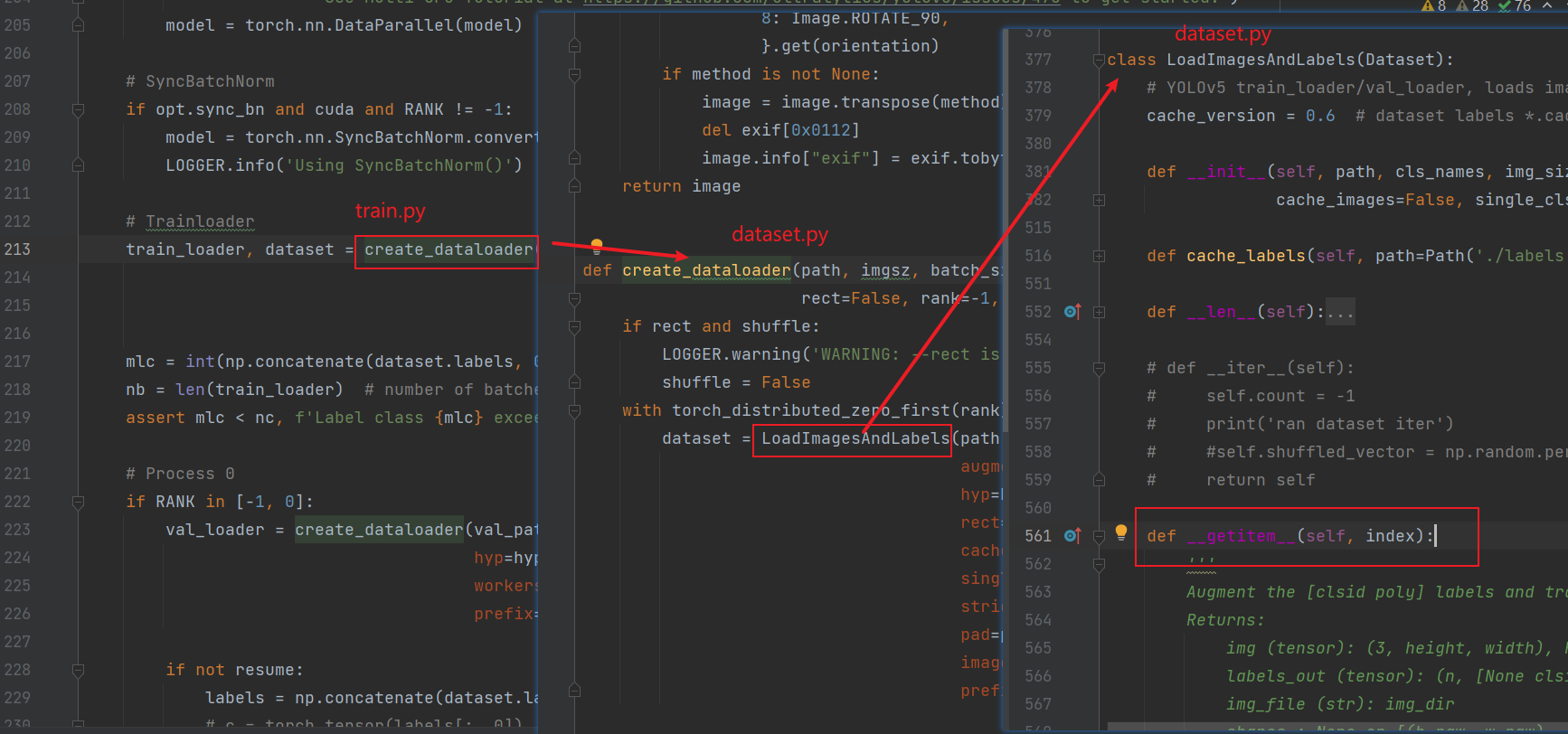
可以看到，取数据的格式和getitem的返回值一致。

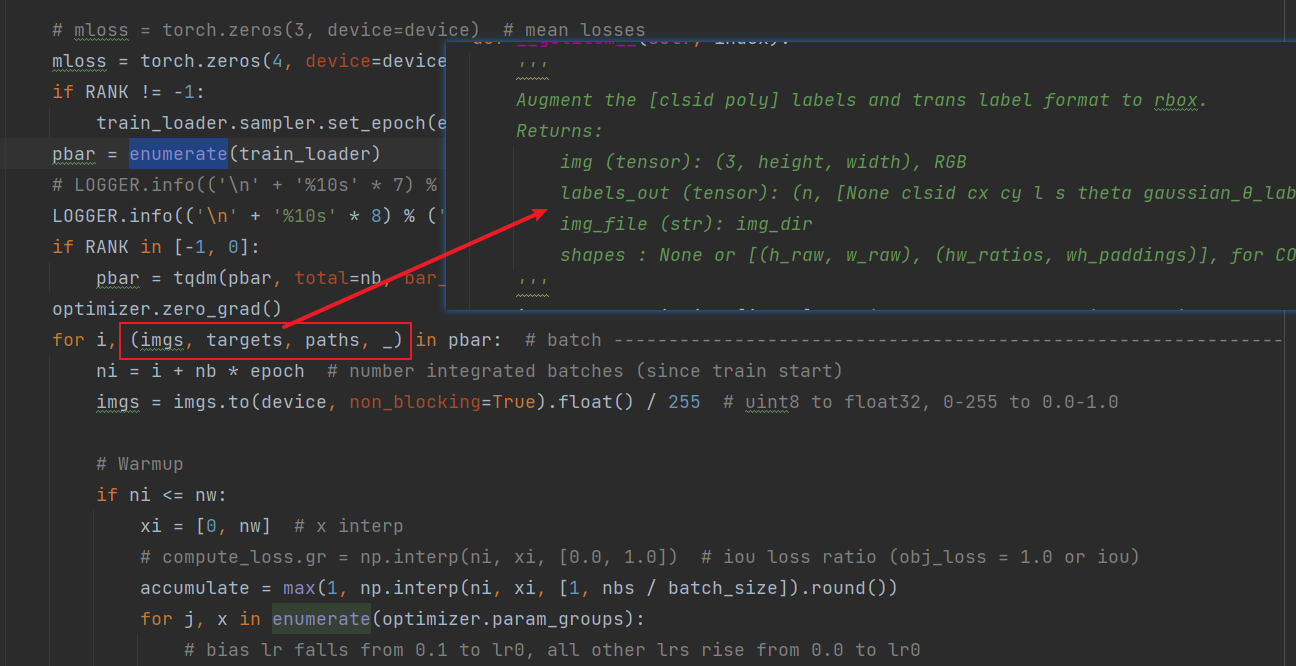
在该方法中，默认启用了csl高斯窗，clsid不上传，在得到bbox之后合并。

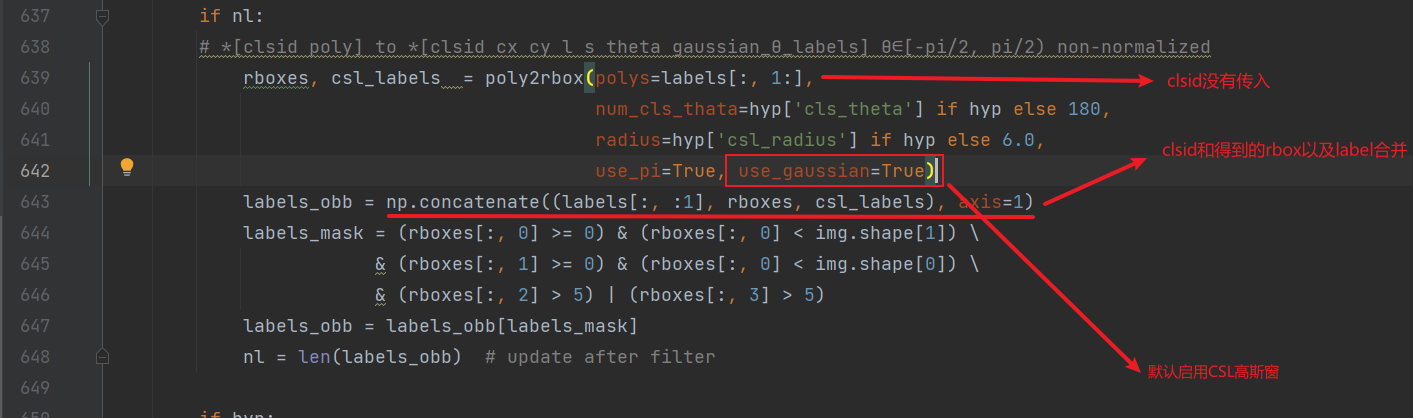
下面我把poly2rbox单独拎出来分析：

import numpy as np
import torch

pi = 3.141592
import cv2


def gaussian_label_cpu(label, num_class, u=0, sig=4.0):
    """
    转换成CSL Labels：
        用高斯窗口函数根据角度θ的周期性赋予gt labels同样的周期性，使得损失函数在计算边界处时可以做到“差值很大但loss很小”；
        并且使得其labels具有环形特征，能够反映各个θ之间的角度距离
    Args:
        label (float32):[1], theta class
        num_theta_class (int): [1], theta class num
        u (float32):[1], μ in gaussian function
        sig (float32):[1], σ in gaussian function, which is window radius for Circular Smooth Label
    Returns:
        csl_label (array): [num_theta_class], gaussian function smooth label
    """
    x = np.arange(-num_class/2, num_class/2)
    y_sig = np.exp(-(x - u) ** 2 / (2 * sig ** 2))
    index = int(num_class/2 - label)
    return np.concatenate([y_sig[index:], 
                           y_sig[:index]], axis=0)


def regular_theta(theta, mode='180', start=-pi/2):
    """
    limit theta ∈ [-pi/2, pi/2)
    """
    assert mode in ['360', '180']
    cycle = 2 * pi if mode == '360' else pi

    theta = theta - start
    theta = theta % cycle
    return theta + start


def poly2rbox(polys, num_cls_thata=180, radius=6.0, use_pi=False, use_gaussian=False):
    """
    Trans poly format to rbox format.
    Args:
        polys (array): (num_gts, [x1 y1 x2 y2 x3 y3 x4 y4])
        num_cls_thata (int): [1], theta class num
        radius (float32): [1], window radius for Circular Smooth Label
        use_pi (bool): True θ∈[-pi/2, pi/2) ， False θ∈[0, 180)

    Returns:
        use_gaussian True:
            rboxes (array):
            csl_labels (array): (num_gts, num_cls_thata)
        elif
            rboxes (array): (num_gts, [cx cy l s θ])
    """
    assert polys.shape[-1] == 8
    if use_gaussian:
        csl_labels = []
    rboxes = []
    for poly in polys:
        poly = np.float32(poly.reshape(4, 2))
        # poly: [[1. 1.], [2. 0.], [5. 4.], [4. 5.]]
        # cv2.minAreaRect求出点集下的最小面积矩形
        (x, y), (w, h), angle = cv2.minAreaRect(poly) # θ ∈ [0， 90]
        angle = -angle # θ ∈ [-90， 0]
        theta = angle / 180 * pi # 转为pi制

        # trans opencv format to longedge format θ ∈ [-pi/2， pi/2]
        if w != max(w, h):
            w, h = h, w
            theta += pi/2
        theta = regular_theta(theta) # limit theta ∈ [-pi/2, pi/2)
        angle = (theta * 180 / pi) + 90 # θ ∈ [0， 180)

        if not use_pi: # 采用angle弧度制 θ ∈ [0， 180)
            rboxes.append([x, y, w, h, angle])
        else: # 采用pi制
            rboxes.append([x, y, w, h, theta])
        if use_gaussian:
            csl_label = gaussian_label_cpu(label=angle, num_class=num_cls_thata, u=0, sig=radius)
            csl_labels.append(csl_label)
    if use_gaussian:
        return np.array(rboxes), np.array(csl_labels)
    return np.array(rboxes)


def main():
    ploys = torch.tensor([[1, 1, 2, 0, 5, 4, 4, 5],
                          [5, 1, 6, 2, 6, 2.5, 5, 1.5]])
    rboxes, csl_labels = poly2rbox(polys=ploys,
                                   num_cls_thata=180,
                                   radius=6.0,
                                   use_pi=True, use_gaussian=True)
    print('rboxes: ', rboxes)
    print('csl_labels: ', csl_labels)


if __name__ == "__main__":
    main()

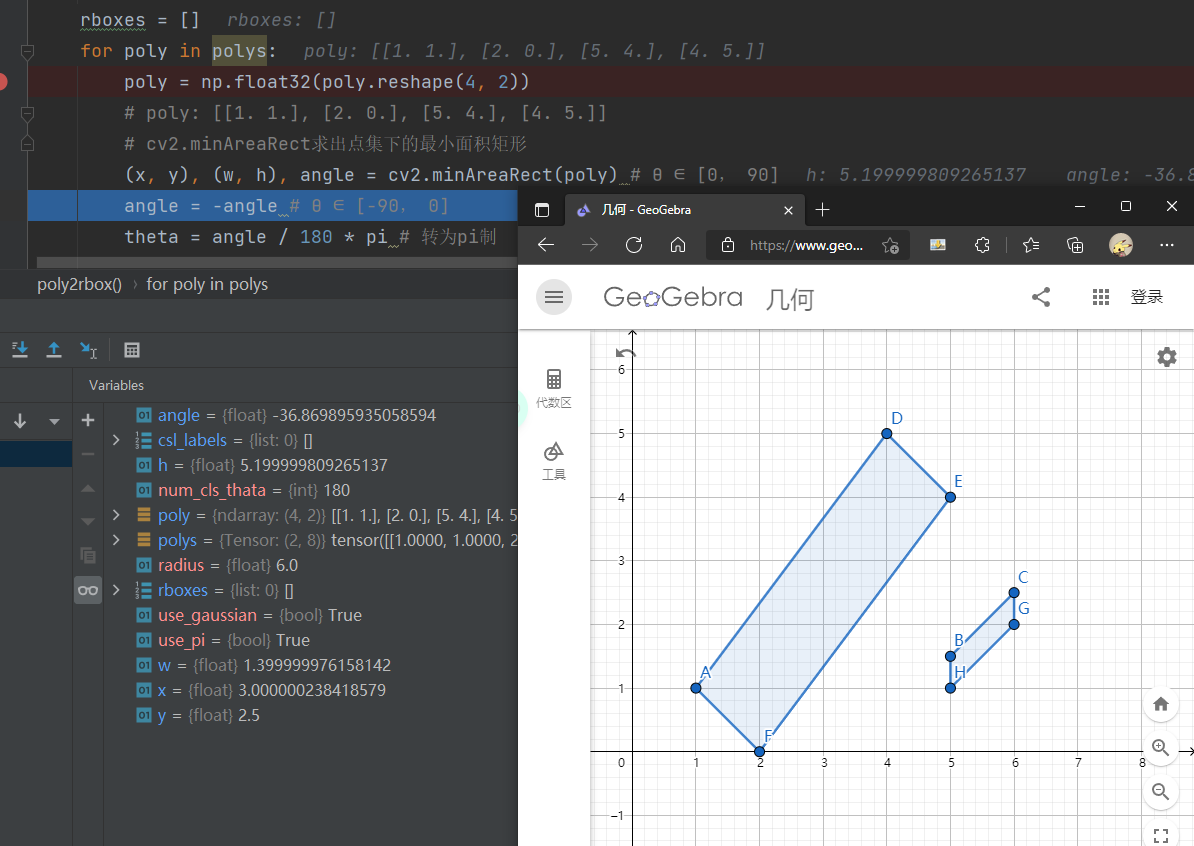
这是debug记录，比较奇怪的是x,y,w,h的计算似乎cv2的api有点问题，比如我给的例子，角度计算的没问题，但是很明显一个3,4,5的三角形，结果h=5.199999；短边1:1:1.414(根号2)，结果算出来是w=1.39。虽然差距不大，本身api的调用确实可能比较复杂（可以实现求点集下最小面积矩形）。当然实际情况是标注的label可能不一定是完美的矩形，用当作矩形的方法似乎也有不妥。但是这对loss的求解和反向传播肯定是有影响的。至此target部分的数据，csl的角度怎么得到的都已经清楚，将在下一篇博客里面探究。pred是如何得到的。另外，这个demo中csl_labels: (2, 180)
图片描述

一、api记录

1.tqdm（进度条美观）

from tqdm import tqdm
import time

iterator = tqdm(iterable=range(100),
                # iterable：tdqm数据参数支持的数据类型是可迭代的对象iterable，
                # 在Python中默认的可迭代对象有：list、str、tuple、dict、file、range等
				desc='test_tqdm',
                # str类型，作为进度条说明，在进度条左边
				total=100,
                # 预取的迭代次数
				leave=True,
                # 循环结束后是否保留进度提示信息，默认保留
				ncols=100,
                # 进度条长度，150比较适合
				mininterval=0.1,
                # 进度条最小的更新间隔（秒）
				maxinterval=10.0,
                # 进度条最大的更新间隔（秒）
				unit='it',
                # 单位，默认it每秒迭代数
				bar_format=None,
				# bar_format='{l_bar}{bar:10}{r_bar}{bar:-10b}',
                # 在进度条右边添加字典类型描述信息
				position=None,
                # 指定偏移，这个功能在多个进度条中有用
				postfix=None
                # 自定义进度条
                )
for i in iterator:
    time.sleep(0.3)

结果如下：
图片描述

2.python专有函数

没有python的基础，所以有些基础知识也是边实践边学（轻喷/-_-\），类似**init函数等的python的专有函数，是在创建一个类对象之后一定会调用的方法，类似于构造函数。同时也可被重载（项目中的get_item**就是重载了专有函数），下面是一个简单的例子。

class Cat:
    def __init__(self, color):
        self.color = color

    def eat(self):
        print("--eating food--")

    def printinfo(self):
        print(self.color)


# 实例化Cat对象
mimi = Cat("white")
# 如果创建实例的时候没有给color，此句会报错
mimi.printinfo()
mimi.eat()
# 重新给类成员赋值
mimi.color = "black"
mimi.printinfo()

输出如下：