HLS学习入门(霍夫圆检测)
学习使用 HLS 设计一个基于 Hough 变换的圆检测算法
一、Hough变换原理
霍夫变换(Hough Transform)是图像处理中的一种特征提取技术,该过程在一个参数空间中通过计算累计结果
的局部最大值得到一个符合该特定形状的集合作为霍夫变换结果。霍夫变换于 1962 年由 Paul Hough 首次提出,后
于 1972 年由 Richard Duda 和 Peter Hart 推广使用,经典霍夫变换用来检测图像中的直线,后来霍夫变换扩展到
任意形状物体的识别,多为圆和椭圆。霍夫变换运用两个坐标空间之间的变换将在一个空间中具有相同形状的曲线
或直线映射到另一个坐标空间的一个点上形成峰值,从而把检测任意形状的问题转化为统计峰值问题。
1.Hough 变换直线检测
简单的说,就是:图像空间中的直线与参数空间中的点是一一对应的,参数空间中的直线与图像空间中的点也是一一对应的
说实话我不是很懂百度或者原文中的原理解释,我的理解就是图像空间中的直线由两个参数(k,b)决定,这两个参数在参数空间反映为1点。反之同理
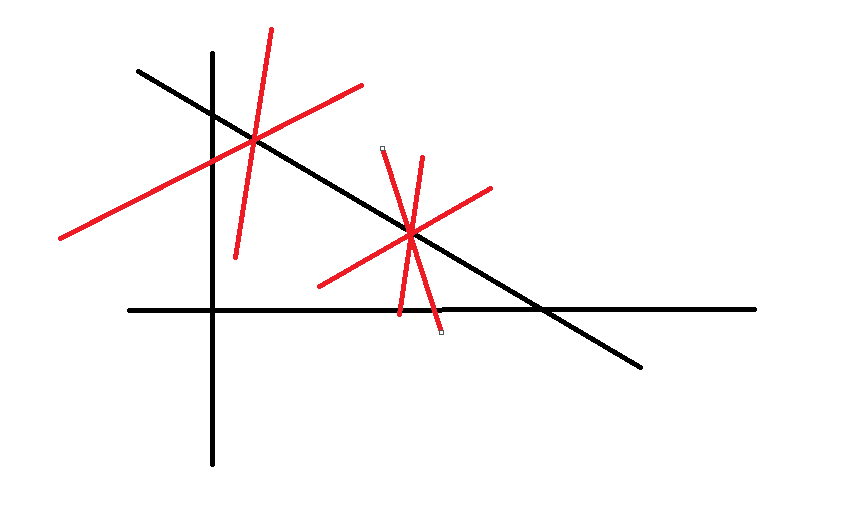
简单的说,比如如图的黑色直线,假定它的参数是[k, b],现在扫描整幅图像上的点,而经过每一个点都有无数条直线(红色),根据前文我们知道每一条图像空间中的直线都对于参数空间的一个点。因为这条直线上的所有点它所产生的直线簇一定有一条经过原直线(即在参数空间会存在一个点[k, b]与之对应),所以,这一趟扫描下来,会在参数空间这得到较为多的对应点[k ,b],据此,我们可以认为原图空间存在这样一条直线与参数空间[k ,b]点相对应。
2.Hough 变换圆检测
继使用 hough 变换检测出直线之后,顺着坐标变换的思路,提出了一种检测圆的方法。
1 如何表示一个圆?
与使用(r,theta)来表示一条直线相似,使用(a,b,r)来确定一个圆心为(a,b)半径为 r 的圆。
2 如何表示过某个点的所有圆?
某个圆过点(x1,y1),则有:(x1-a1)^2 + (y1-b1)^2 = r1^2 。
那么过点(x1,y1)的所有圆可以表示为(a1(i),b1(i),r1(i)),其中 r1∈(0,无穷),每一个 i 值都对应一个
不同的圆,(a1(i),b1(i),r1(i))表示了无穷多个过点(x1,y1)的圆。
3 如何确定多个点在同一个圆上?
如(2)中说明,过点(x1,y1)的所有圆可以表示为(a1(i),b1(i),r1(i)),过点(x2,y2)的所有圆可以表示为
(a2(i),b2(i),r2(i)),过点(x3,y3)的所有圆可以表示为(a3(i),b3(i),r3(i)),如果这三个点在同一个圆
上 , 那 么 存 在 一 个 值 ( a0,b0,r0 ) , 使 得 a0 = a1(k)=a2(k)=a3(k) 且 b0 = b1(k)=b2(k)=b3(k) 且 r0
= r1(k)=r2(k)=r3(k),即这三个点同时在圆(a0,b0,r0)上。
从下图可以形象的看出:
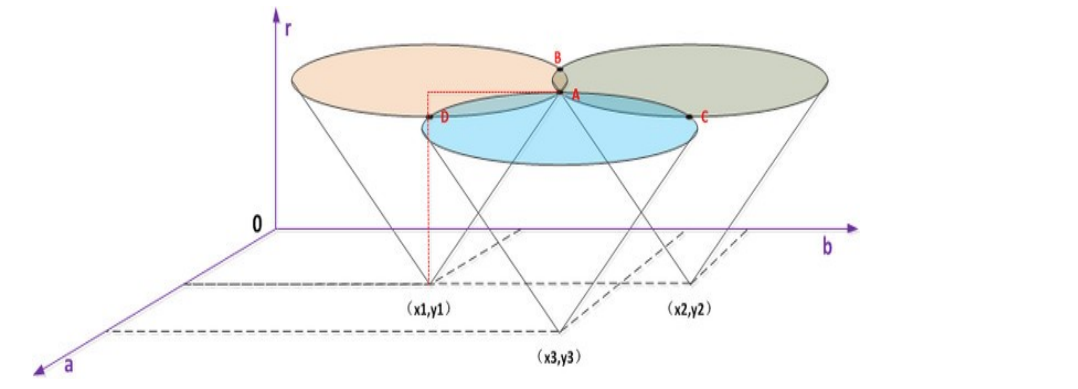
首先,分析过点(x1,y1)的所有圆(a1(i),b1(i),r1(i)),当确定 r1(i)时 ,(a1(i),b1(i))的轨迹是一
个以(x1,y1,r1(i))为中心半径为 r1(i)的圆。那么,所有圆(a1(i),b1(i),r1(i))的组成了一个以(x1,y1,0)
为顶点,锥角为 90 度的圆锥面。
三个圆锥面的交点 A 既是同时过这三个点的圆。
3.Hough 变换圆检测流程
Hough 变换时一种利用图像的全局特征将特定形状边缘链接起来。它通过点线的对偶性,将源图像上的点影射
到用于累加的参数空间,把原始图像中给定曲线的检测问题转化为寻找参数空间中的峰值问题。由于利用全局特征,
所以受噪声和边界间断的影响较小,比较鲁棒。
Hough 变换思想为:在原始图像坐标系下的一个点对应了参数坐标系中的一条直线,同样参数坐标系的一条直
线对应了原始坐标系下的一个点,然后,原始坐标系下呈现直线的所有点,它们的斜率和截距是相同的,所以它们
在参数坐标系下对应于同一个点。这样在将原始坐标系下的各个点投影到参数坐标系下之后,看参数坐标系下有没
有聚集点,这样的聚集点就对应了原始坐标系下的直线。
因此采用 hough 变换主要有以下几个步骤:
1)Detect the edge
检测得到图像的边缘
2)Create accumulator
采用二维向量描述图像上每一条直线区域,将图像上的直线区域计数器映射到参数空间中的存储单元,p 为直
线区域到原点的距离,所以对于对角线长度为 n 的图像,p 的取值范围为(0, n),θ 值得取值范围为(0, 360),
定义为二维数组 HoughBuf[n][360]为存储单元。
对所有像素点(x,y)在所有 θ 角的时候,求出ρ.从而累加ρ值出现的次数。高于某个阈值的ρ就是一个直
线。这个过程就类似于横坐标是 θ 角,ρ就是到直线的最短距离。横坐标 θ 不断变换,根据直线方程公司,ρ =
xcosθ + ysinθ 对于所有的不为 0 的像素点,计算出ρ,找到ρ在坐标(θ,ρ)的位置累加 1.
3) Detect the peaks, maximal in the accumulator
通过统计特性,假如图像平面上有两条直线,那么最终会出现 2 个峰值,累加得到最高的数组的值为所求直线
参数
二、Hough圆检测的HLS实现
我们看下面一个实际问题:我们要从一副图像中检测出半径以知的圆形来。我们可以取和图像平面一样的参数
平面,以图像上每一个前景点为圆心,以已知的半径在参数平面上画圆,并把结果进行累加。最后找出参数平面上
的峰值点,这个位置就对应了图像上的圆心。在这个问题里,图像平面上的每一点对应到参数平面上的一个圆。
把上面的问题改一下,假如我们不知道半径的值,而要找出图像上的圆来。这样,一个办法是把参数平面扩大
称为三维空间。就是说,参数空间变为 x–y–R 三维,对应圆的圆心和半径。图像平面上的每一点就对应于参数空
间中每个半径下的一个圆,这实际上是一个圆锥。最后当然还是找参数空间中的峰值点。不过,这个方法显然需要
大量的存储空间,运行速度也会是很大问题。
那么有什么比较好的解决方法么?我们前面假定的图像都是黑白图像(二值图像),实际上这些二值图像多是彩
色或灰度图像通过边缘提取来的。我们前面提到过,图像边缘除了位置信息,还有方向信息也很重要,这里就用上
了。根据圆的性质,圆的半径一定在垂直于圆的切线的直线上,也就是说, 在圆上任意一点的法线上。这样,解
决上面的问题,我们仍采用 2 维的参数空间,对于图像上的每 一前景点,加上它的方向信息,都可以确定出一条
直线,圆的圆心就在这条直线上。这样一来,问题就会简单了许多
三、代码解析
#include "top.h"
//#include "opencv_top.h"
#include <stdio.h>
#include <iostream>
using namespace std;
void hls::hls_hough_line(GRAY_IMAGE &src,GRAY_IMAGE &dst,int rows,int cols)
{
GRAY_PIXEL result;
int row ,col,k;
///参数空间的参数圆心O(a,b)半径radius
int a = 0,b = 0,radius = 0;
//累加器
int A0 = rows;
int B0 = cols;
//注意HLS不支持变长数组,所以这里直接指定数据长度
const int Size = 1089900;//Size = rows*cols*(120-110);
#ifdef __SYNTHESIS__
int _count[Size];
int *count = &_count[0];
#else
//这一步在HLS中不能被综合,仅仿真使用
int *count =(int *) malloc(Size * sizeof(int));
#endif
//偏移
int index ;
//为累加器赋值0
for (row = 0;row < Size;row++)
{
count[row] = 0;
}
GRAY_PIXEL src_data;
uchar temp0;
for (row = 0; row< rows;row++)
{
#pragma HLS PIPELINE II=1 off
for (col = 0; col< cols;col++)
{
src >> src_data;
uchar temp = src_data.val[0];
//检测黑线
if (temp == 0)
{
//遍历a ,b 为;累加器赋值
for (a = 0;a < A0;a++)
{
for (b = 0;b < B0;b++)
{
radius = (int)(sqrt(pow((double)(row-a),(double)2) + pow((double)(col - b),(double)2)));
if(radius > 110 && radius < 120)
{
index = A0 * B0 *(radius-110) + A0*b + a;
count[index]++;
}
}
}
}
}
}
//遍历累加器数组,找出所有的圆
for (a = 0 ; a < A0 ; a++)
{
#pragma HLS PIPELINE II=1 off
for (b = 0 ; b < B0; b++)
{
for (radius = 110 ; radius < 120; radius++)
{
index = A0 * B0 *(radius-110) + A0*b + a;
if (count[index] > 210)
{
//在image2中绘制该圆
for(k = 0; k < rows;k++)
{
for (col = 0 ; col< cols;col++)
{
//x有两个值,根据圆公式(x-a)^2+(y-b)^2=r^2得到
int temp = (int)(sqrt(pow((double)radius,(double)2)- pow((double)(col-b),(double)2)));
int x1 = a + temp;
int x2 = a - temp;
if ( (k == x1)||(k == x2) ){
result.val[0] = (uchar)255;
}
else{
result.val[0] = (uchar)0;
}
dst << result;
}
}
}
}
}
}
}
void hls_hough(AXI_STREAM& src_axi, AXI_STREAM& dst_axi, int rows, int cols)
{
#pragma HLS INTERFACE axis port=src_axi
#pragma HLS INTERFACE axis port=dst_axi
#pragma HLS RESOURCE core=AXI_SLAVE variable=rows metadata="-bus_bundle CONTROL_BUS"
#pragma HLS RESOURCE core=AXI_SLAVE variable=cols metadata="-bus_bundle CONTROL_BUS"
#pragma HLS RESOURCE core=AXI_SLAVE variable=return metadata="-bus_bundle CONTROL_BUS"
#pragma HLS INTERFACE ap_stable port=rows
#pragma HLS INTERFACE ap_stable port=cols
GRAY_IMAGE img_src(rows, cols);
GRAY_IMAGE img_dst(rows, cols);
#pragma HLS dataflow
hls::AXIvideo2Mat(src_axi,img_src);
hls::hls_hough_line(img_src,img_dst,rows,cols);
hls::Mat2AXIvideo(img_dst,dst_axi);
}
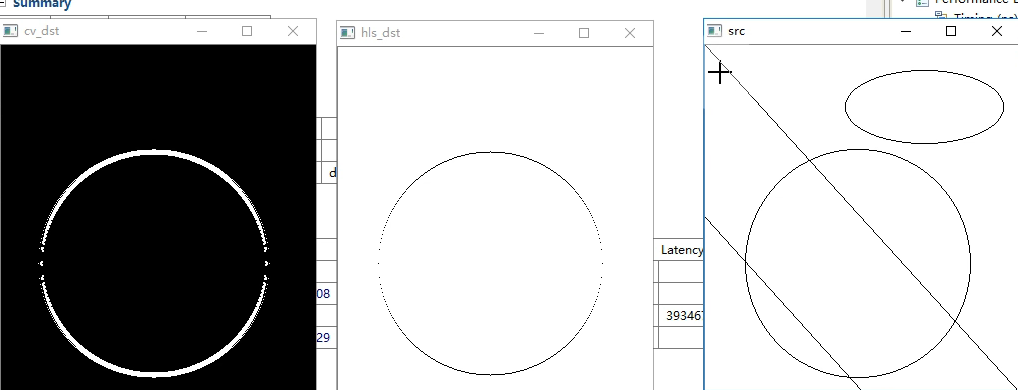
四、仿真结果